RC -sarjan piirin yksityiskohtainen analyysi
2024-05-08
20533
RC -sarjan piiri, joka koostuu vastuksesta ja kondensaattorista, toimii peruskomponenttina sekä perus- että edistyneissä elektronisissa järjestelmäsuunnissa.Se auttaa ymmärtämään keskeisiä periaatteita, kuten taajuusvastetta, vaihesiirtoa ja signaalin suodatusta, joilla on merkittävä rooli piirisuunnittelussa ja signaalinkäsittelyssä.Tämä etsintä kattaa teoreettiset perusteet ja ulottuu käytännön sovelluksiin kokeiden ja simulaatioiden avulla.Kokoamalla piiri tai mallintamalla sitä digitaalisesti, oppijat voivat visuaalisesti ymmärtää latausprosessia ja komponentin Variat -ionien vaikutuksia, mikä tekee monimutkaisista käsitteistä helpompia ja ikimuistoisia.
Luettelo
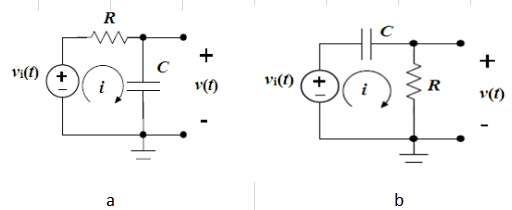
Kuva 1: RC -piirien erilaiset lähtöjännitteet
Johdanto RC -piiriin
RC-piiri, lyhenne, vastus kaatamispiirille, on elektroniikan perustana signaalien manipuloimiseksi vastusten ja kondensaattorien kautta.Nämä piirit tunnetaan erityisesti kyvystään siirtää vaiheita ja suodatinsignaaleja käyttämällä näiden komponenttien yksinkertaisia järjestelyjä.Perus RC-piiri, jota usein kutsutaan ensimmäisen asteen RC-piiriksi, sisältää tyypillisesti vain yhden vastuksen ja yhden kondensaattorin.
Tyypillisessä asennuksessa tulojännite kohdistetaan vastuksen ja kondensaattorin sarjajärjestelyyn.Lähtö voidaan piirtää joko vastuksen tai kondensaattorin yli, jokainen antaa erilaisia vasteita signaalitaajuuksille kondensaattorin ainutlaatuisten ominaisuuksien vuoksi.Tämä monipuolisuus antaa RC -piirejä suorittaa erilaisia rooleja elektronisissa laitteissa, kuten kytkentä- ja suodatussignaalit tai jopa muuntavat aaltomuodot, kun niille kohdistuu askeljännite.
RC-piiri voidaan konfiguroida monin tavoin-sarjat, rinnakkaiset tai molempien yhdistelmä, joka tunnetaan nimellä sarja-selkä.Jokainen kokoonpano vaikuttaa signaalitaajuuksiin eri tavalla: Sarjayhteydet yleensä heikentävät matalia taajuuksia, kun taas rinnakkaisliitäntöjä käytetään korkeampien taajuuksien vaimentamiseen.Tämä ero johtuu pääasiassa tapaa, jolla vastukset ja kondensaattorit ovat vuorovaikutuksessa piirin kanssa;Vastukset vastustavat suoraan virtaa, kun kondensaattorit tallentavat ja vapauttavat sen, vaikuttaen siihen, miten piiri reagoi eri taajuuksiin.
Toisin kuin piireissä, jotka sisältävät induktoreita, kuten LC -piirejä, yksinkertaiset RC -piirit eivät voi resonoida, koska vastukset eivät säilytä energiaa.Tämä ominaisuus vaikuttaa selvästi siihen, miten RC -piirejä käytetään, keskittyen niiden kapasiteettiin suodattamiseen energian varastoinnin tai resonanssin sijasta.Jokainen kokoonpano palvelee tiettyä tarkoitusta, mikä tekee RC -piireistä monipuolisia työkaluja sekä teoreettisessa tutkimuksessa että käytännöllisessä sovelluksessa sähköisessä suunnittelussa.
RC -sarjapiiri
RC -sarjan piiri, joka koostuu pääasiassa vastuksesta (R -) ja kondensaattori (C) Sarjassa toimii suoraviivaisella periaatteella.Kun piirin kytkin on suljettu, kondensaattori alkaa latautua käytetystä jännitteestä (V), aloittamalla virran virtaus piirin läpi.Kondensaattorin varauksen yhteydessä virta kasvaa vähitellen, kunnes kondensaattori saavuttaa kapasiteettinsa, jolloin se lopettaa varauksen ja virran vakiintuminen sen maksimiarvossa, laskettuna 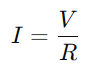 .
.
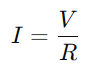 .
.Kondensaattorin latausprosessi voidaan kuvata matemaattisesti yhtälöllä  , missä olen nykyinen, V on jännite, R - on vastus, C on kapasitanssi, t on aika, ja e on luonnollisen logaritmin perusta.Tämä kaava heijastaa sitä, kuinka virta muuttuu ajan kuluessa kondensaattorin varautuessa, ja resistanssi- ja kapasitanssiarvojen (RC) tuote määrittelee piirin aikavakion, mikä osoittaa kondensaattorin varauksen nopeuden.
, missä olen nykyinen, V on jännite, R - on vastus, C on kapasitanssi, t on aika, ja e on luonnollisen logaritmin perusta.Tämä kaava heijastaa sitä, kuinka virta muuttuu ajan kuluessa kondensaattorin varautuessa, ja resistanssi- ja kapasitanssiarvojen (RC) tuote määrittelee piirin aikavakion, mikä osoittaa kondensaattorin varauksen nopeuden.
 , missä olen nykyinen, V on jännite, R - on vastus, C on kapasitanssi, t on aika, ja e on luonnollisen logaritmin perusta.Tämä kaava heijastaa sitä, kuinka virta muuttuu ajan kuluessa kondensaattorin varautuessa, ja resistanssi- ja kapasitanssiarvojen (RC) tuote määrittelee piirin aikavakion, mikä osoittaa kondensaattorin varauksen nopeuden.
, missä olen nykyinen, V on jännite, R - on vastus, C on kapasitanssi, t on aika, ja e on luonnollisen logaritmin perusta.Tämä kaava heijastaa sitä, kuinka virta muuttuu ajan kuluessa kondensaattorin varautuessa, ja resistanssi- ja kapasitanssiarvojen (RC) tuote määrittelee piirin aikavakion, mikä osoittaa kondensaattorin varauksen nopeuden.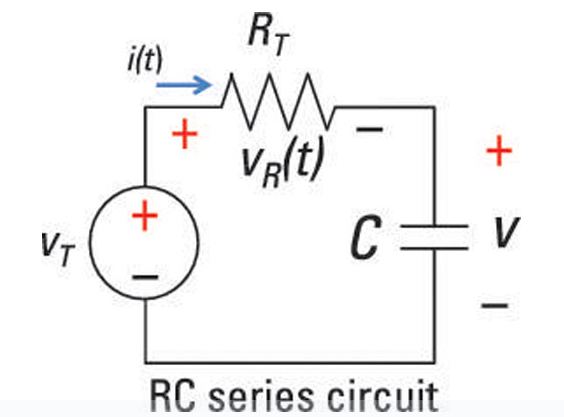
Kuva 2: RC -sarjan piiri
Purkaminen tapahtuu, kun kytkin avataan, prosessin kääntäminen: kondensaattorin tallennettu energia vapautuu, aiheuttaen virran virtauksen vastakkaiseen suuntaan, kunnes kondensaattori on tyhjennetty.Tämä lataus- ja purkamisjakso on ratkaisevan tärkeä sovelluksissa, kuten signaalin muuntaminen, suodatus ja ajoituspiirit, johtuen ennakoitavissa olevasta tavasta, jolla virran ja jännitteen muutos.
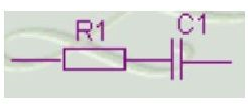
Kuva 3: RC -sarjan oikosulku
RC -sarjapiirin käyttäytyminen vaihtelee myös taajuuden mukaan.Matalalla taajuuksilla kondensaattori toimii enemmän kuin avoin piiri, mikä estää suuresti virran virtausta.Taajuus lisääntyessä kapasitiivinen reaktanssi pienenee, mikä helpottaa virran läpi.Tämä impedanssin muutos taajuudella mahdollistaa RC -sarjan piirin toimia suodattimena, heikentäen selektiivisesti taajuuksia tietyn kynnyksen alapuolella (kääntötaajuus  ).
).
 ).
).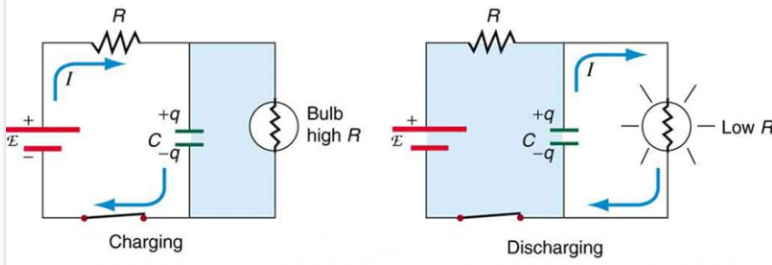
Kuva 4: RC -sarjan piirien lataaminen ja purkaminen
Vakaan tilan toimintojen lisäksi RC-piirejä tutkitaan myös niiden ohimenevien vasteiden suhteen, kun ne tehdään äkillisille jännitemuutoksille, kuten silloin, kun tasavirtalähde kytketään päälle tai pois päältä.Tätä skenaariota kutsutaan ohimeneväksi prosessiksi, jossa piiri siirtyy vakasta tilasta toiseen.Tämän prosessin dynamiikka riippuu merkittävästi RC -aikavakiosta, joka säätelee kuinka nopeasti piiri reagoi muutoksiin.
Viime kädessä RC -sarjan piirit palvelevat useita toimintoja sekä tasavirta- että AC -sovelluksissa, käsittelevät tehtäviä signaalien viivästymisestä eri piirielementtien integrointiin tai kytkemiseen.Tämä monipuolisuus johtuu vastuksen ja kondensaattorin välisistä ainutlaatuisista vuorovaikutuksista, jotka yhdessä määrittävät piirin kokonaisvasteen jännitteen ja taajuuden muutoksiin.
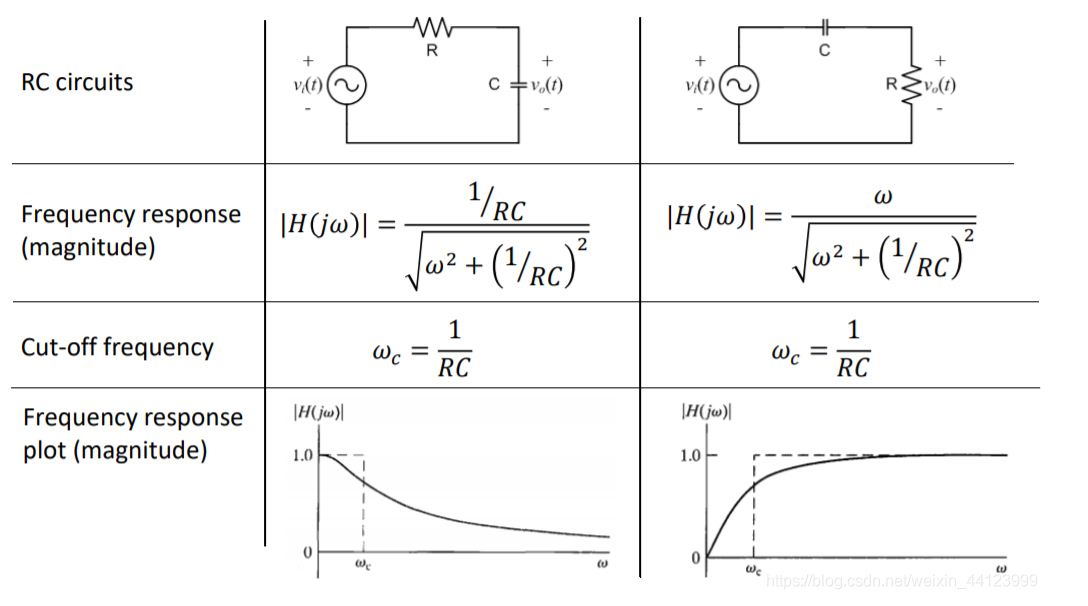
Kuva 5: RC -sarjan piirikaavio ja taajuuskaava
RC -sarjan piirissä vastuksen välinen vuorovaikutus (R) ja kondensaattori (C) vaikuttaa sekä virran virtaukseen että jännitteen jakautumiseen.Vastuksen ensisijainen rooli on säätää nykyistä virtausta.Tämä suhde määritetään Ohmin laki, joka toteaa 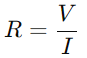 missä V on jännite ja Minä on nykyinen.Pohjimmiltaan vastus toimii pullonkaulana, hallitsemalla kuinka paljon sähköä voi kulkea läpi milloin tahansa.
missä V on jännite ja Minä on nykyinen.Pohjimmiltaan vastus toimii pullonkaulana, hallitsemalla kuinka paljon sähköä voi kulkea läpi milloin tahansa.
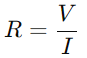 missä V on jännite ja Minä on nykyinen.Pohjimmiltaan vastus toimii pullonkaulana, hallitsemalla kuinka paljon sähköä voi kulkea läpi milloin tahansa.
missä V on jännite ja Minä on nykyinen.Pohjimmiltaan vastus toimii pullonkaulana, hallitsemalla kuinka paljon sähköä voi kulkea läpi milloin tahansa.Kondensaattorin toiminto on hiukan monimutkaisempi, koska se tallentaa väliaikaisesti sähköenergiaa ja vapauttaa sen sitten takaisin piiriin.Jännite kondensaattorin yli (Pääomanpäällikkö) korreloi varastoidun varauksensa kanssa (Q -) ja lasketaan kaavaa käyttämällä 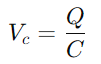 .Tämä suhde korostaa kondensaattorin kykyä pitää varausta, mikä vaikuttaa suoraan sen esittämiin jännitteisiin.Toiminnan aikana kondensaattorin lataamisen ja purkamisen dynamiikka on välttämätöntä RC -piireiden ymmärtämiseksi.Aikavakio (τ), määritelty
.Tämä suhde korostaa kondensaattorin kykyä pitää varausta, mikä vaikuttaa suoraan sen esittämiin jännitteisiin.Toiminnan aikana kondensaattorin lataamisen ja purkamisen dynamiikka on välttämätöntä RC -piireiden ymmärtämiseksi.Aikavakio (τ), määritelty 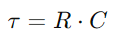 , mittaa, kuinka nopeasti kondensaattori saavuttaa noin 63,2% lähteen toimittamasta koko jännitteestä (V0 -).Tämä aikavakio viittaa siihen, kuinka piiri sopeutuu tulonmuutoksiin, kun vastuksen ja kondensaattorin ominaisuudet määräävät näiden säätöjen vauhtia.
, mittaa, kuinka nopeasti kondensaattori saavuttaa noin 63,2% lähteen toimittamasta koko jännitteestä (V0 -).Tämä aikavakio viittaa siihen, kuinka piiri sopeutuu tulonmuutoksiin, kun vastuksen ja kondensaattorin ominaisuudet määräävät näiden säätöjen vauhtia.
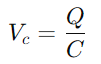 .Tämä suhde korostaa kondensaattorin kykyä pitää varausta, mikä vaikuttaa suoraan sen esittämiin jännitteisiin.Toiminnan aikana kondensaattorin lataamisen ja purkamisen dynamiikka on välttämätöntä RC -piireiden ymmärtämiseksi.Aikavakio (τ), määritelty
.Tämä suhde korostaa kondensaattorin kykyä pitää varausta, mikä vaikuttaa suoraan sen esittämiin jännitteisiin.Toiminnan aikana kondensaattorin lataamisen ja purkamisen dynamiikka on välttämätöntä RC -piireiden ymmärtämiseksi.Aikavakio (τ), määritelty 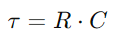 , mittaa, kuinka nopeasti kondensaattori saavuttaa noin 63,2% lähteen toimittamasta koko jännitteestä (V0 -).Tämä aikavakio viittaa siihen, kuinka piiri sopeutuu tulonmuutoksiin, kun vastuksen ja kondensaattorin ominaisuudet määräävät näiden säätöjen vauhtia.
, mittaa, kuinka nopeasti kondensaattori saavuttaa noin 63,2% lähteen toimittamasta koko jännitteestä (V0 -).Tämä aikavakio viittaa siihen, kuinka piiri sopeutuu tulonmuutoksiin, kun vastuksen ja kondensaattorin ominaisuudet määräävät näiden säätöjen vauhtia.Jännite kondensaattorin yli milloin tahansa latauksen aikana on annettu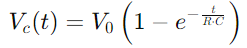 , havainnollistaa epälineaarista kasvua kondensaattorin täyttöä.Tämä yhtälö kuvaa, kuinka varausnopeus hidastuu kondensaattorin lähestyessä täydellistä kapasiteettia.
, havainnollistaa epälineaarista kasvua kondensaattorin täyttöä.Tämä yhtälö kuvaa, kuinka varausnopeus hidastuu kondensaattorin lähestyessä täydellistä kapasiteettia.
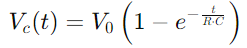 , havainnollistaa epälineaarista kasvua kondensaattorin täyttöä.Tämä yhtälö kuvaa, kuinka varausnopeus hidastuu kondensaattorin lähestyessä täydellistä kapasiteettia.
, havainnollistaa epälineaarista kasvua kondensaattorin täyttöä.Tämä yhtälö kuvaa, kuinka varausnopeus hidastuu kondensaattorin lähestyessä täydellistä kapasiteettia.Kondensaattorin jännite laskee päinvastoin kuin vastuuvapauden aikana 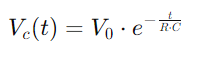 , kuvataan varastoidun energian lineaarista vähenemistä ajan myötä.Tämä prosessi tarjoaa selkeän kuvan siitä, kuinka energia vapautetaan kondensaattorista takaisin piiriin.Vaihtovirtasovelluksissa vaiheen ja virran välinen vaiheero, φ, tulee kriittinen.Tämä ero, laskettuna
, kuvataan varastoidun energian lineaarista vähenemistä ajan myötä.Tämä prosessi tarjoaa selkeän kuvan siitä, kuinka energia vapautetaan kondensaattorista takaisin piiriin.Vaihtovirtasovelluksissa vaiheen ja virran välinen vaiheero, φ, tulee kriittinen.Tämä ero, laskettuna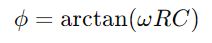 jossa ω edustaa kulmataajuutta, näyttää kondensaattorin aiheuttaman viiveen, joka vaikuttaa ajoitukseen, kun virtavirrat ja jännitteet muuttuvat komponenttien välillä.
jossa ω edustaa kulmataajuutta, näyttää kondensaattorin aiheuttaman viiveen, joka vaikuttaa ajoitukseen, kun virtavirrat ja jännitteet muuttuvat komponenttien välillä.
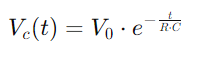 , kuvataan varastoidun energian lineaarista vähenemistä ajan myötä.Tämä prosessi tarjoaa selkeän kuvan siitä, kuinka energia vapautetaan kondensaattorista takaisin piiriin.Vaihtovirtasovelluksissa vaiheen ja virran välinen vaiheero, φ, tulee kriittinen.Tämä ero, laskettuna
, kuvataan varastoidun energian lineaarista vähenemistä ajan myötä.Tämä prosessi tarjoaa selkeän kuvan siitä, kuinka energia vapautetaan kondensaattorista takaisin piiriin.Vaihtovirtasovelluksissa vaiheen ja virran välinen vaiheero, φ, tulee kriittinen.Tämä ero, laskettuna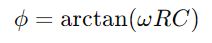 jossa ω edustaa kulmataajuutta, näyttää kondensaattorin aiheuttaman viiveen, joka vaikuttaa ajoitukseen, kun virtavirrat ja jännitteet muuttuvat komponenttien välillä.
jossa ω edustaa kulmataajuutta, näyttää kondensaattorin aiheuttaman viiveen, joka vaikuttaa ajoitukseen, kun virtavirrat ja jännitteet muuttuvat komponenttien välillä.Kaiken kaikkiaan vastus rajoittaa ja ohjaa virran virtausta, kun kondensaattori tallentaa ja moduloi jännitettä.Yhdessä ne määrittelevät piirin vaste -ominaisuudet, kuten kuinka nopeasti se voi ladata ja purkaa, ja vaihekappaleet, jotka tapahtuvat vuorotellen virran skenaarioissa.Tämä yhdistetty käyttäytyminen tukee RC -sarjan piirien perustoimintaa, mikä tekee niistä olennaisia erilaisia elektronisia sovelluksia.
RC -sarjan piirin perusyhtälöt
RC -sarjapiirin käyttäytymisen ymmärtämiseksi on välttämätöntä aloittaa perusyhtälöillä, jotka kuvaavat sen vastetta tulojännitteen muutoksiin.Oletetaan, että meillä on muuttuva tulojännite Vin (t), kun jännite vastus on merkitty VR (T) ja kondensaattorin koko VC (T).Sarjapiirissä sama virta, Se) Virtaa sekä vastuksen että kondensaattorin läpi.
Kirchhoffin jännitelain (KVL) soveltaminen, jonka mukaan piirin suljetun silmukan ympärillä olevan kokonaisjännitteen on oltava nolla, havaitsemme, että tulojännite on yhtä suuri kuin vastuksen ja kondensaattorin jännitteiden summa:
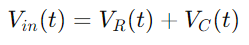
Jännite vastuksen yli voidaan laskea Ohmin laki:

Kondensaattorille jännitteen VC (t) liittyy siihen, että sillä on varaus Q (t): Annetaan:
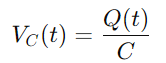
Koska virta on määritelty varausvirtana, meillä on:
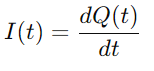
Korvaamalla Q (t) yhtälöllä jtk VC (T)ja varauksen johdannainen Se), johdetaan RC -sarjan piirin ytimen differentiaaliyhtälö:
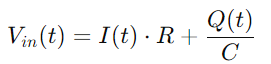
Edelleen korvaaminen Q (t) olennaisesti Se), saamme:
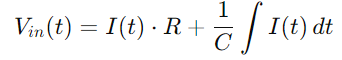
Virta -I (T): lle, kun otetaan huomioon kondensaattorin jännitteen muutosnopeus, käytämme:
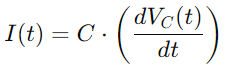
Kaikkien näiden suhteiden integrointi antaa meille differentiaaliyhtälön, joka kuvaa kondensaattorin jännitettä:
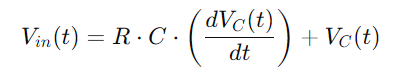
Tämä on ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö, joka vangitsee ajasta riippuvan jännitteen muutoksen kondensaattorin yli.Tämän yhtälön ratkaiseminen antaa meille mahdollisuuden kuvata tarkasti, kuinka kondensaattorijännite kehittyy.Tämä ymmärrys on olennainen kondensaattorin lataus- että purkamisjaksojen analysoimiseksi, samoin kuin piirin vaste eri taajuuksille.Tämä kattava lähestymistapa tarjoaa syvän kuvan RC -sarjan piirin dynaamisista ominaisuuksista.
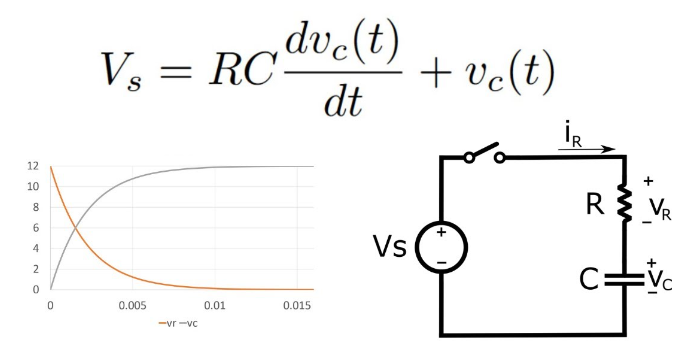
Kuva 6: Jänniteerot yhtälö
RC -sarjapiirin impedanssi
RC-sarjan piirin kuvauksen kirjoittamiseksi keskittymällä ihmisen vuorovaikutukseen ja suoriin, yksinkertaistettuihin selityksiin, tehostamme konkreettisia kokemuksia ja askel askeleelta operaatioita ylläpitämällä ydinviestiä ja johdonmukaisuutta:
RC -sarjan piirissä vastus ja kondensaattori työskentelevät samanaikaisesti sähkön virtauksen hallitsemiseksi, mikä on ratkaisevan tärkeää vaihtoehtoisten virtojen kanssa.Piirin kokonaisimpedanssi, edustettuna 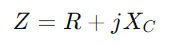 , yhdistää resistenssin R ja kapasitiivinen reaktanssi XC.Tämän asennuksen avainominaisuus on, että molempien komponenttien impedanssiarvot vaihtelevat taajuuden muutosten mukaan.Taajuuden kasvaessa kondensaattorin impedanssi laskee, mikä antaa enemmän virtaa kulkea läpi, kun taas vastus pysyy olennaisesti vakiona.
, yhdistää resistenssin R ja kapasitiivinen reaktanssi XC.Tämän asennuksen avainominaisuus on, että molempien komponenttien impedanssiarvot vaihtelevat taajuuden muutosten mukaan.Taajuuden kasvaessa kondensaattorin impedanssi laskee, mikä antaa enemmän virtaa kulkea läpi, kun taas vastus pysyy olennaisesti vakiona.
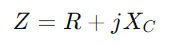 , yhdistää resistenssin R ja kapasitiivinen reaktanssi XC.Tämän asennuksen avainominaisuus on, että molempien komponenttien impedanssiarvot vaihtelevat taajuuden muutosten mukaan.Taajuuden kasvaessa kondensaattorin impedanssi laskee, mikä antaa enemmän virtaa kulkea läpi, kun taas vastus pysyy olennaisesti vakiona.
, yhdistää resistenssin R ja kapasitiivinen reaktanssi XC.Tämän asennuksen avainominaisuus on, että molempien komponenttien impedanssiarvot vaihtelevat taajuuden muutosten mukaan.Taajuuden kasvaessa kondensaattorin impedanssi laskee, mikä antaa enemmän virtaa kulkea läpi, kun taas vastus pysyy olennaisesti vakiona.Impedanssi, nimeltään Z -z ja mitattuna ohmeina (ω) on kriittinen rooli määritettäessä, kuinka piiri reagoi vuorottelevaan virtaan.Kuten RL -sarjan piireissä, vastus R - ja kapasitiivinen reaktanssi xC RC -piiristä muodostaa kolmion, joka tunnetaan nimellä impedanssikolmio.Tämä kolmio liittyy läheisesti jännite kolmioon, ja levittämällä Pythagoran lause voit laskea piirin kokonaisimpedanssin.
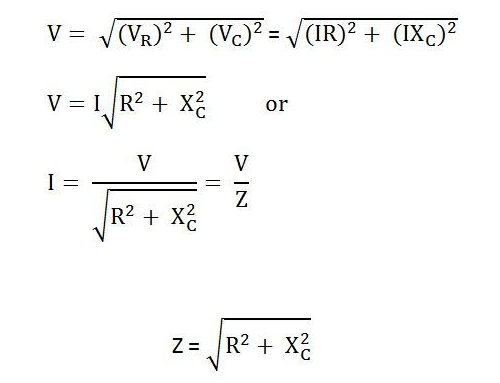
Kuva 7: RC -sarjan piirilaskentakaava
Kun kyse on käytännön sovelluksista, harkitse kuulokkeita, jotka käyttävät näitä periaatteita.Korkean impedanssin kuulokkeita, jotka ylittävät usein 200 ohmia, käytetään tyypillisesti pöytätietokoneiden, virtavahvistimien ja ammatillisten äänilaitteiden kanssa.Nämä korkean impedanssimallit vastaavat hyvin ammattitason elektroniikan lähtöominaisuuksia.Näitä kuulokkeita käytettäessä on välttämätöntä säätää äänenvoimakkuutta vähitellen, jotta vältetään herkän sisäisen komponentin, kuten äänikelan, ylikuormittaminen ja vahingoittaminen.
Päinvastoin, matalan impedanssin kuulokkeet, yleensä alle 50 ohmia, ovat parempia kannettaville laitteille, kuten CD-soittimille, MD-soittimille tai MP3-soittimille.Nämä kuulokkeet vaativat vähemmän virtaa korkealaatuisen äänen tuottamiseksi, mikä tekee niistä ihanteellisia mobiililaitteiden käyttöön.Ne vaativat kuitenkin myös huolellista huomiota herkkyystasoihin optimaalisen suorituskyvyn varmistamiseksi ja kuulokkeiden tai kuulon vaurioiden estämiseksi.
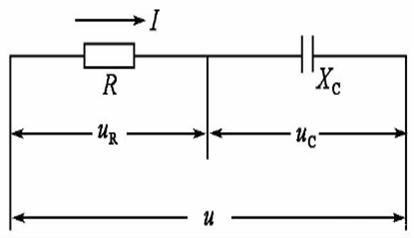
Kuva 8: RC -sarjan piirin impedanssikaavio
RC -sarjan piireiden sisäänpääsy- ja analysointimenetelmät
Päästömittaus mittaa, kuinka helposti RC -sarjan piiri voi johtaa sähköä, laskettuna impedanssin käänteiseksi (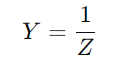 ).Tämä arvo integroi sekä vastus (R -) ja reaktanssi (X) piiristä.Kestävyys vastustaa virran virtausta muuttamalla sähköenergiaa lämmöksi, kun taas reaktanssi tallentaa energiaa väliaikaisesti piiriin.
).Tämä arvo integroi sekä vastus (R -) ja reaktanssi (X) piiristä.Kestävyys vastustaa virran virtausta muuttamalla sähköenergiaa lämmöksi, kun taas reaktanssi tallentaa energiaa väliaikaisesti piiriin.
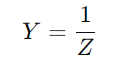 ).Tämä arvo integroi sekä vastus (R -) ja reaktanssi (X) piiristä.Kestävyys vastustaa virran virtausta muuttamalla sähköenergiaa lämmöksi, kun taas reaktanssi tallentaa energiaa väliaikaisesti piiriin.
).Tämä arvo integroi sekä vastus (R -) ja reaktanssi (X) piiristä.Kestävyys vastustaa virran virtausta muuttamalla sähköenergiaa lämmöksi, kun taas reaktanssi tallentaa energiaa väliaikaisesti piiriin.Laskea pääsy
Aloita kirjoittamalla impedanssi 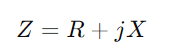 , missä R tarkoittaa vastustuskykyä, X ja reaktanssille ja j - on kuvitteellinen yksikkö.Käytä kaavaa y = 1/(R - Tai jx).Tämä toimenpide sisältää kompleksilukuja ja antaa meille
, missä R tarkoittaa vastustuskykyä, X ja reaktanssille ja j - on kuvitteellinen yksikkö.Käytä kaavaa y = 1/(R - Tai jx).Tämä toimenpide sisältää kompleksilukuja ja antaa meille 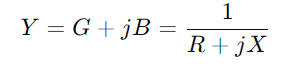 .Tässä, G on johtavuus (todellinen virran virtauskyky) ja B - on herkkä (piirin kyky reagoida virran muutoksiin).
.Tässä, G on johtavuus (todellinen virran virtauskyky) ja B - on herkkä (piirin kyky reagoida virran muutoksiin).
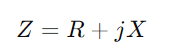 , missä R tarkoittaa vastustuskykyä, X ja reaktanssille ja j - on kuvitteellinen yksikkö.Käytä kaavaa y = 1/(R - Tai jx).Tämä toimenpide sisältää kompleksilukuja ja antaa meille
, missä R tarkoittaa vastustuskykyä, X ja reaktanssille ja j - on kuvitteellinen yksikkö.Käytä kaavaa y = 1/(R - Tai jx).Tämä toimenpide sisältää kompleksilukuja ja antaa meille 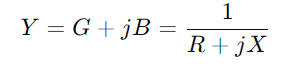 .Tässä, G on johtavuus (todellinen virran virtauskyky) ja B - on herkkä (piirin kyky reagoida virran muutoksiin).
.Tässä, G on johtavuus (todellinen virran virtauskyky) ja B - on herkkä (piirin kyky reagoida virran muutoksiin).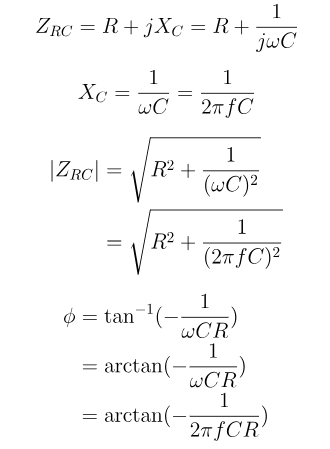
Kuva 9: Sarja RC -piirin impedanssilaskin
Tämä laskelma ei paljasta piirin johtavuutta, vaan myös sen dynaamisia vaste -ominaisuuksia, jotka ovat tärkeitä vaihtovirtapiirin analyysissä.Yhdessä otettu johtavuus ja alttius osoittavat, kuinka piiri ohittaa virran ja miten se varastoi ja vapauttaa energiaa.

Kuva 10: Vaihekulmakaava
Käytännöllinen soveltaminen
Insinöörit käyttävät sisäänpääsyarvoja piirin suunnittelun parantamiseksi, etenkin korkeataajuisissa sovelluksissa, kuten radiotaajuuspiirissä.Päästöjen säätäminen auttaa impedanssin sovittamisessa, signaalin heijastuksen vähentämisessä ja lähetystehokkuuden lisäämisessä.
Tutkimalla pääsyvastetta insinöörit voivat arvioida ja ennustaa piirin suorituskykyä erilaisissa olosuhteissa, kuten taajuusvaste, stabiilisuus ja herkkyys.Varusta oskilloskoopilla ja signaaligeneraattorilla piirin jännitteen ja virran mittaamiseksi vaihtelevilla taajuuksilla.Keskity erityisesti rajataajuuteen teoreettisten ennusteiden testaamiseksi ja validoimalla ne käytännön havaintoihin.Aloita vaihtovirtapiirien määrittämällä kondensaattorin reaktanssi (XC) 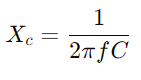 missä f on signaalitaajuus.Laske koko impedanssi
missä f on signaalitaajuus.Laske koko impedanssi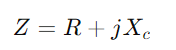 ja sitten pääsy
ja sitten pääsy 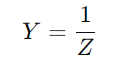 .
.
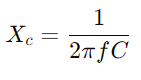 missä f on signaalitaajuus.Laske koko impedanssi
missä f on signaalitaajuus.Laske koko impedanssi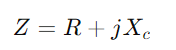 ja sitten pääsy
ja sitten pääsy 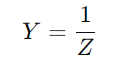 .
.Analysoi vaiheero käyttämällä 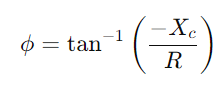 signaalin muodon muutoksen ymmärtäminen.Tutki, kuinka piiri käsittelee erilaisia taajuuksia, erityisesti käyttäytymisen merkitseminen rajataajuudella
signaalin muodon muutoksen ymmärtäminen.Tutki, kuinka piiri käsittelee erilaisia taajuuksia, erityisesti käyttäytymisen merkitseminen rajataajuudella  , missä piiri siirtyy siirtymisestä lohko -signaaleihin.Arviointi, kuinka impedanssi ja vaiheero vaihtelevat taajuuden mukaan, on ratkaisevan tärkeää tehokkaiden suodattimien ja signaaliprosessorien suunnittelussa.Keskustele siitä, kuinka taajuuden selektiivisyys, vaihesiirto ja signaalin vaimennus piirin ominaisuuksista johtuvat käytännöllisistä sovelluksista, kuten suodatus ja elektroninen viritys.
, missä piiri siirtyy siirtymisestä lohko -signaaleihin.Arviointi, kuinka impedanssi ja vaiheero vaihtelevat taajuuden mukaan, on ratkaisevan tärkeää tehokkaiden suodattimien ja signaaliprosessorien suunnittelussa.Keskustele siitä, kuinka taajuuden selektiivisyys, vaihesiirto ja signaalin vaimennus piirin ominaisuuksista johtuvat käytännöllisistä sovelluksista, kuten suodatus ja elektroninen viritys.
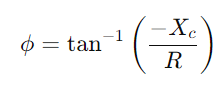 signaalin muodon muutoksen ymmärtäminen.Tutki, kuinka piiri käsittelee erilaisia taajuuksia, erityisesti käyttäytymisen merkitseminen rajataajuudella
signaalin muodon muutoksen ymmärtäminen.Tutki, kuinka piiri käsittelee erilaisia taajuuksia, erityisesti käyttäytymisen merkitseminen rajataajuudella  , missä piiri siirtyy siirtymisestä lohko -signaaleihin.Arviointi, kuinka impedanssi ja vaiheero vaihtelevat taajuuden mukaan, on ratkaisevan tärkeää tehokkaiden suodattimien ja signaaliprosessorien suunnittelussa.Keskustele siitä, kuinka taajuuden selektiivisyys, vaihesiirto ja signaalin vaimennus piirin ominaisuuksista johtuvat käytännöllisistä sovelluksista, kuten suodatus ja elektroninen viritys.
, missä piiri siirtyy siirtymisestä lohko -signaaleihin.Arviointi, kuinka impedanssi ja vaiheero vaihtelevat taajuuden mukaan, on ratkaisevan tärkeää tehokkaiden suodattimien ja signaaliprosessorien suunnittelussa.Keskustele siitä, kuinka taajuuden selektiivisyys, vaihesiirto ja signaalin vaimennus piirin ominaisuuksista johtuvat käytännöllisistä sovelluksista, kuten suodatus ja elektroninen viritys.Tämä lähestymistapa hajottaa toimintaprosessit hallittavissa oleviin vaiheisiin, rikastuttaen käyttäjän ymmärrystä käytännöllisillä tietosuojalla RC -sarjan piirien käsittelemiseen ja analysointiin.
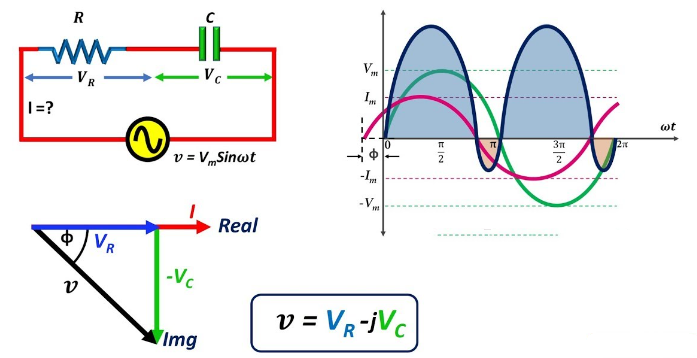
Kuva 11: RC -sarjan piirien ominaisuudet
RC -sarjan piirin fasorikaavio
RC -sarjan piirissä kaikilla elementeillä on sama virta niiden sarjan kokoonpanon vuoksi.Tämä yhtenäinen virta toimii fasorikaaviomme lähtökohtana, joka auttaa visualisoimaan piirin eri jännitteiden ja virtojen välistä suhdetta.Määritetään tämä virta Minä Vertailuhenkilöksi, sijoitettuna nollaasteessa kaavioon.Kaaviossa nykyinen Minä on asetettu vaakasuoraan oikealle, määrittäen nollaasteen referenssiviivan.Jännite vastuksen poikki (OaR -) on vaiheessa virran kanssa, koska vastukset eivät aiheuta mitään vaihesiirtoa.Siten, OaR - vedetään vaakasuoraan vektoriksi samaan suuntaan kuin Minä, ulottuu alkuperästä.
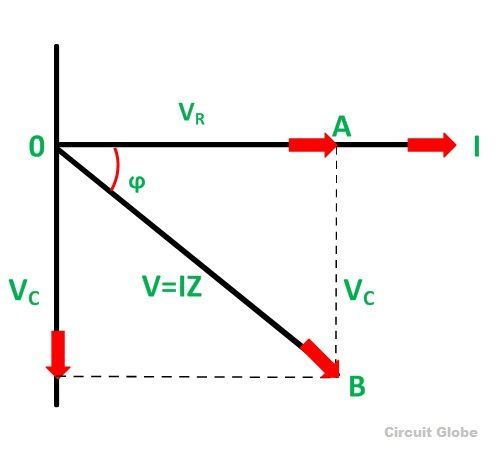
Kuva 12: RC -sarjan piirikaavio kaavio
Sitä vastoin kondensaattorin jännite (OaC) johtaa virt astetta johtuen nykyisen vaiheen viivästymisen kapasitiivisesta ominaisuudesta.Tätä jännitettä edustaa pystysuora vektori, joka osoittaa ylöspäin, alkaen kärjestä OaR - vektori.Kokonaisjännite Oa piirissä on vektorisumma Oa Rannikko OaC.Tämä summa muodostaa oikean kolmion OaR - ja OaC viereisinä ja vastakkaisina puolina.Tämän kolmion hypotenuse, joka ulottuu alkuperästä OaC vektori, edustaa Oa.
Sinusoidinen virta piirin läpi annetaan synnillä (ωt), missä im on suurin virran amplitudi ja ω on kulmataajuus.Näin ollen vastuksen jännite on 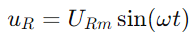 , Nykyisen aaltomuodon heijastaminen.Jännite kondensaattorin yli on annettu
, Nykyisen aaltomuodon heijastaminen.Jännite kondensaattorin yli on annettu 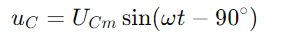 , osoittaen vaihesiirron −90 ° (tai 90 astetta virran edessä).Phasor -kaavion oikea kolmio selventää sitä
, osoittaen vaihesiirron −90 ° (tai 90 astetta virran edessä).Phasor -kaavion oikea kolmio selventää sitä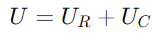 ei ole vain suuruusluokassa, vaan myös vaihesuhteessa, päätejännitevektorin kanssa (Oa) kolmion suorittaminen.
ei ole vain suuruusluokassa, vaan myös vaihesuhteessa, päätejännitevektorin kanssa (Oa) kolmion suorittaminen.
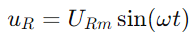 , Nykyisen aaltomuodon heijastaminen.Jännite kondensaattorin yli on annettu
, Nykyisen aaltomuodon heijastaminen.Jännite kondensaattorin yli on annettu 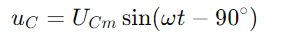 , osoittaen vaihesiirron −90 ° (tai 90 astetta virran edessä).Phasor -kaavion oikea kolmio selventää sitä
, osoittaen vaihesiirron −90 ° (tai 90 astetta virran edessä).Phasor -kaavion oikea kolmio selventää sitä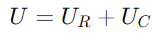 ei ole vain suuruusluokassa, vaan myös vaihesuhteessa, päätejännitevektorin kanssa (Oa) kolmion suorittaminen.
ei ole vain suuruusluokassa, vaan myös vaihesuhteessa, päätejännitevektorin kanssa (Oa) kolmion suorittaminen.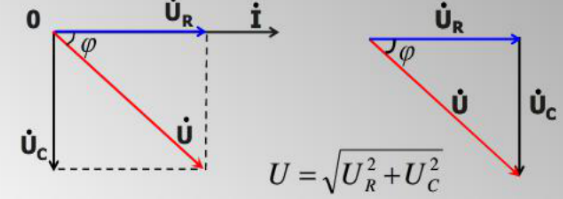
Kuva 13: RC -sarjan piirin jännitekagrammi
Avainkohdat sarjan RC -piirejen analysoinnissa
Impedanssi sarjan RC -piirissä, edustettuna Z -z, yhdistää vastus (R -) ja kapasitanssin reaktiivinen vaikutus yhdeksi mittaksi, joka vaihtelee signaalitaajuuden mukaan.Se ilmaistaan matemaattisesti 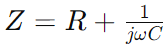 missä ω on kulmataajuus ja C on kapasitanssi.Tässä, R - muodostaa impedanssin todellisen osan ja
missä ω on kulmataajuus ja C on kapasitanssi.Tässä, R - muodostaa impedanssin todellisen osan ja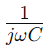 edustaa kuvitteellista osaa, mikä osoittaa, kuinka kondensaattori vaikuttaa piiriin.
edustaa kuvitteellista osaa, mikä osoittaa, kuinka kondensaattori vaikuttaa piiriin.
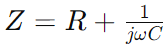 missä ω on kulmataajuus ja C on kapasitanssi.Tässä, R - muodostaa impedanssin todellisen osan ja
missä ω on kulmataajuus ja C on kapasitanssi.Tässä, R - muodostaa impedanssin todellisen osan ja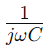 edustaa kuvitteellista osaa, mikä osoittaa, kuinka kondensaattori vaikuttaa piiriin.
edustaa kuvitteellista osaa, mikä osoittaa, kuinka kondensaattori vaikuttaa piiriin.Tapa impedanssimuutokset taajuudella on keskeinen RC -piirien käyttämiseen suodatussovelluksissa.Pienemmillä taajuuksilla piirissä on suurempi impedanssi, joka estää nämä taajuudet tehokkaasti.Sitä vastoin korkeammilla taajuuksilla impedanssi laskee, jolloin nämä taajuudet pääsevät vapaammin.Tämä käyttäytyminen tekee sarjasta RC-piirit, jotka ovat ihanteellisia tehtäviin, kuten ei-toivottujen matalataajuisen melun suodattamiseen tai korkean taajuuden signaalien ohittamiseen.
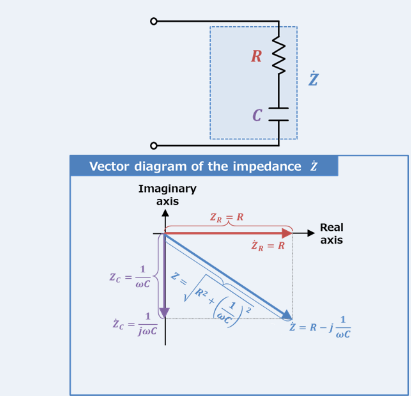
Kuva 14: RC -sarjan piirin impedanssivektorikaavio
Johtopäätös
Ei -toivottujen taajuuksien suodattamisesta signaalivasteisiin RC -sarjan piiri on tärkeä osa elektronisia toimintoja.Ymmärtämällä näiden piirien, insinöörit ja suunnittelijat on varustettu käsityöratkaisuihin, jotka hallitsevat signaalin eheyttä monimutkaisissa elektronisissa järjestelmissä.Näiden piirejen yksityiskohtainen tutkimus, jota tukevat matemaattiset analyysit ja visuaaliset esitykset, kuten Phasor -kaaviot, tarjoaa kattavan kuvan, joka on tärkeä kaikille, jotka haluavat syventää ymmärrystään elektronisesta piirin dynamiikasta tai parantaa heidän käytännön taitojaan piirisuunnittelussa ja vianetsinnässä.
Usein kysyttyjä kysymyksiä [UKK]
1. Mikä on RC -piirin periaate?
RC: n (vastus-kondensaattorin) piirin periaate pyörii kondensaattorin lataus- ja purkamisprosessien ympärillä vastuksen läpi.Tässä piirissä kondensaattorin kyky tallentaa ja vapauttaa sähköenergiaa on vuorovaikutuksessa vastuksen kanssa, joka hallitsee nopeutta, jolla kondensaattori lataa tai purkautuu.
2. Miksi RC -piiri johtaa virtaa?
RC -piirissä virta johtaa jännitteen kondensaattorin yli, koska kondensaattorin on aloitettava lataus ennen kuin sen jännite voi nousta.Koska virta virtaa kondensaattoriin sen lataamiseksi, virran huippu on ennen kuin kondensaattorin jännite saavuttaa maksiminsa.Tämä vaikutus aiheuttaa vaihesiirron, jossa virranvaihe johtaa jännitekaasua jopa 90 asteeseen tulosignaalin taajuudesta riippuen.
3. Kuinka jännitteen muutos RC -piirissä?
Jännitteen muutos RC -piirissä latauksen aikana kuvataan eksponentiaalisella toiminnolla.Kun jännitettä käytetään, kondensaattorin välinen jännite kasvaa alun perin nopeasti, sitten hidastuu lähestyessään syöttöjännitettä.Matemaattisesti tämä ilmaistaan 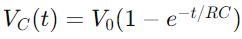 missä VC(t) on jännite kondensaattorin läpi ajankohtana T, V0 on syöttöjännite ja RC on piirin aikavakio, määrittäen, kuinka nopeasti kondensaattorin varaukset.Sitä vastoin purkautumisen aikana kondensaattorin jännitteet vähenevät eksponentiaalisesti yhtälön jälkeen
missä VC(t) on jännite kondensaattorin läpi ajankohtana T, V0 on syöttöjännite ja RC on piirin aikavakio, määrittäen, kuinka nopeasti kondensaattorin varaukset.Sitä vastoin purkautumisen aikana kondensaattorin jännitteet vähenevät eksponentiaalisesti yhtälön jälkeen 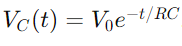 .
.
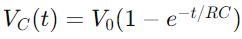 missä VC(t) on jännite kondensaattorin läpi ajankohtana T, V0 on syöttöjännite ja RC on piirin aikavakio, määrittäen, kuinka nopeasti kondensaattorin varaukset.Sitä vastoin purkautumisen aikana kondensaattorin jännitteet vähenevät eksponentiaalisesti yhtälön jälkeen
missä VC(t) on jännite kondensaattorin läpi ajankohtana T, V0 on syöttöjännite ja RC on piirin aikavakio, määrittäen, kuinka nopeasti kondensaattorin varaukset.Sitä vastoin purkautumisen aikana kondensaattorin jännitteet vähenevät eksponentiaalisesti yhtälön jälkeen 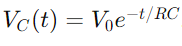 .
. MEISTä
Asiakastyytyväisyys joka kerta.Keskinäinen luottamus ja yhteiset edut.
MEISTä
Asiakastyytyväisyys joka kerta.Keskinäinen luottamus ja yhteiset edut.
toimivuustesti.Suurimmat kustannustehokkaat tuotteet ja paras palvelu ovat iankaikkinen sitoutumisemme.
Kuuma artikkeli
- Ovat CR2032 ja CR2016 vaihdettavissa
- MOSFET: Määritelmä, työperiaate ja valinta
- Releiden asennus ja testaus, relejyhtymiskaavioiden tulkinta
- CR2016 vs. CR2032 Mikä on ero
- NPN vs. PNP: Mikä ero on?
- ESP32 vs STM32: Mikä mikrokontrolleri on sinulle parempi?
- LM358 Dual Operatiivinen vahvistin Kattava opas: Pinoutit, piirikaaviot, ekvivalentit, hyödylliset esimerkit
- CR2032 vs DL2032 vs CR2025 Vertailuopas
- Ymmärtäminen ESP32- ja ESP32-S3: n teknisten ja suorituskykyanalyysien ymmärtäminen
- RC -sarjan piirin yksityiskohtainen analyysi
 1N4148-diodien perusteellinen analyysi: toimintatavat, tekniset tiedot ja käyttöskenaariot
1N4148-diodien perusteellinen analyysi: toimintatavat, tekniset tiedot ja käyttöskenaariot
2024-05-08
 Dynaamisten ja positiivisten siirtymäpumppujen tyypit ja käyttötarkoitukset
Dynaamisten ja positiivisten siirtymäpumppujen tyypit ja käyttötarkoitukset
2024-05-07
Kuuma osanumero
 EMK105SD222JV-F
EMK105SD222JV-F CL10C010CB8NNNC
CL10C010CB8NNNC 2220CC274KAT1A
2220CC274KAT1A GRM32RR71E225KA01K
GRM32RR71E225KA01K CL10C040CB8NNNC
CL10C040CB8NNNC CC0402GRNPO9BN221
CC0402GRNPO9BN221 0603YC821MAT2A
0603YC821MAT2A CGA4F2X7R2A222M085AE
CGA4F2X7R2A222M085AE GRJ31BR73A471KWJ1L
GRJ31BR73A471KWJ1L 1812CC683MAT1A
1812CC683MAT1A
- XM2S-2511
- SUM45N25-58-E3
- 2N3904
- MAX1238EEE+T
- IDT71256SA15PZ
- PIC12F675-I/MF
- MAX4132EUA
- VI-J7R-EY
- 2MBI100J-120
- MCC19-04IO1B
- HMC431LP4ETR
- TMS320DM6437ZWTQ4
- IS43DR81280C-25DBLI-TR
- MP7748DF-LF-Z
- DS90UB936TRGZTQ1
- TS1852ID
- TPS54395PWPR
- AD7718BRZ-REEL7
- STM32F769BIT6
- SS24T3G
- AM79C30AJC/E
- CN3010-500BG564-SCP-Y-G
- IMP813LESA
- LEON-G100-05S
- M29F200B-70N1
- MB89535APF-G-1035E1
- SAA7826HL/E/M1A
- SAB8031A-N
- SC90089VL
- SMM766BFT-1109L
- TDA7705DCM
- TLE4250-2G
- VSC7145XRU-34
- VT222CR-ADJ
- W9864G6JH-7
- NLNSE70129D-125BGC
- IDGH1G-04A1F1C-14X
- MPC89L515AF
- VENUE2-103N